Introduzione alla climatologia: elementi di statistica descrittiva – Misure di tendenza centrale – Parte settima

Nell’articolo della settimana scorsa abbiamo introdotto la mediana e nello specifico abbiamo analizzato le metodologie di calcolo a seconda delle caratteristiche principali della distribuzione dei dati osservati, mettendo chiaramente in evidenza come il calcolo non sia così scontato come per le medie algebriche.

In questo articolo analizziamo, invece, le proprietà, le caratteristiche e i difetti di questo indice di posizione, con una breve analisi di chiusura concernente il confronto fra media aritmetica semplice e mediana.

Una prima proprietà della mediana, anche abbastanza intuitiva, è rappresentata dalla particolarità che, in una distribuzione di dati, ogni valore che venga estratto in modo casuale, ha la stessa probabilità di essere maggiore o minore rispetto a tale indice di posizione.

Apparentemente questo dettaglio potrà sembrare di poco valore ma come vedremo in futuri articoli di Statistica matematica, esso risulta di particolare importanza quando si analizza in modo dettagliato una distribuzione di dati e, soprattutto, quando si fanno confronti fra valori appartenenti a campioni diversi.

Una seconda proprietà della mediana è rappresentata dal fatto che, quando i dati sono in numero dispari, essa, a differenza della media, per la quale ciò è vero solo in presenza di particolari distribuzioni riconducibili a determinate progressioni matematiche, difficilmente riscontrabili nei fenomeni reali, essa è un valore realmente osservato nella popolazione o campione in esame, e non un valore, come si dice, mediato.

Un’ulteriore proprietà, di valore strettamente matematico, ma di fondamentale importanza legato al suo utilizzo, è quella che tale indice di posizione è l’unico valore di una distribuzione di dati che minimizza la somma degli scarti presi in valore assoluto.

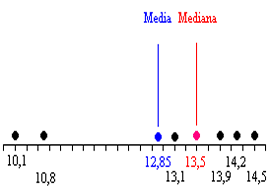
Per meglio comprendere ulteriori proprietà e alcuni difetti di questo indice di tendenza centrale, il lettore si concentri nell’immagine in allegato che rappresenta il significato geometrico di una serie di dati, così composta [10,1;10,8;13,1;13,9;14,2;14,5], mediante la rappresentazione numerica attraverso una retta reale contenente gli elementi della serie per i quali si è provveduto a calcolarne la media aritmetica semplice (12,85) e la mediana (13,50).

Appare di immediata percezione visiva come la somma della distanza dalla media dei valori collocati prima di essa, sia uguale alla somma della distanza dei valori collocati dopo di essa.

In tal modo abbiamo dimostrato, anche attraverso l’ausilio grafico, come la media aritmetica corrisponde al punto di bilanciamento o di equilibrio dei dati, cioè rappresenta il baricentro della distribuzione equiripartendo il fenomeno tra le unità statistiche.

La mediana, invece, appare evidente come sia collocata tra i valori maggiormente addensati, essendo determinata dalle modalità centrali ove cioè le frequenze relative risultano essere prevalenti rispetto alle code di una distribuzione, nel caso di distribuzioni uniformi intorno ai valori centrali.

Questo raffronto tra media e mediana implica alcune considerazioni assai importanti sulle quali occorre focalizzare l’attenzione.

La mediana, essendo determinata dalle modalità centrali, è estremamente sensibile alle modifiche indotte nel corpo centrale della distribuzione e, pertanto, va utilizzata con estrema cautela quando la differenza tra due popolazioni o campioni è rilevante proprio nel centro della distribuzione ordinata delle modalità.

Essa presenta pertanto la capacità di essere rappresentativa della posizione della distribuzione, a differenza della media, anche in presenza di valori estremi notevolmente diversi da tutti gli altri; tale requisito è detto resistenza e deriva dal fatto che il suo calcolo tiene conto solo dell’ordinamento delle osservazioni limitandosi a considerare la modalità dell’elemento collocato al centro della graduatoria ordinata.

Nel caso di dati distribuiti in modo non simmetrico, la mediana rappresenta in modo più adeguato della media l’addensamento dei dati, il valore normale o tipico della serie in quanto la media è maggiormente influenzata dalla presenza dei due valori più distanti, che la allontanano dal gruppo dei valori più frequenti e la rendono diversa da essi.

Ad esempio, in riferimento all’immagine allegata, se i due valori anomali fossero più vicini (o più lontani), rispetto agli altri quattro, la media cambierebbe mentre la mediana rimarrebbe invariata.

Mi permetto di sottolineare in chiusura come un uso opportunistico di tali indici (media e mediana) possa portare a conclusioni di parte in una analisi statistica non corretta o incompleta, che il lettore è bene sappia riconoscere.

Infatti, essendo la media aritmetica baricentro della distribuzione dei dati, essa risulterà fortemente enfatizzata, in valore e nel suo utilizzo, da parte di chi vuole focalizzare maggiormente l’attenzione sulle situazioni nelle quali contano, a parità numerica, gli estremi molto più dei valori centrali.

A differenza, essendo la mediana piuttosto resistente ai valori estremi, essa risulterà fortemente enfatizzata, in valore e nel suo utilizzo, da parte di chi vuole focalizzare maggiormente l’attenzione sulle situazioni nelle quali contano, a parità numerica, i valori centrali molto più dei valori estremi.

Come vedremo in articoli futuri, proprio per evitare queste situazioni poco oggettive, l’utilizzo di tali indici di posizione deve seguire rigorose regole statistiche vincolate soprattutto al tipo di distribuzione matematica che meglio approssima il fenomeno reale oggetto di studio … e questo vale anche in climatologia !

Bibliografia :

Statistica per le decisioni
Piccolo D.
Il Mulino

Statistica applicata alla ricerca biologica ed ambientale
Prof. Soliani L.
Uni Nova Editore