Spesso si discute del fatto che i modelli non riescono a cogliere le caratteristiche di un particolare evento meteorologico sul bacino del Mediterraneo, a causa dell’imprecisa rappresentazione dell’orografia. In effetti, una buona descrizione dei rilievi, su un’area come l’Italia, è certamente uno degli ingredienti necessari per giungere ad una buona previsione, soprattutto per alcuni tipi di eventi, quali cicloni orografici, passaggi di fronti sulle Alpi, fenomeni di blocco sopravvento, precipitazioni orografiche, ecc.
Sostanzialmente, la precisione con cui un modello meteorologico può vedere l’orografia è legata alla risoluzione della griglia del modello stesso. Quindi i modelli globali avranno solo una descrizione “grossolana” delle montagne, mentre i modelli ad area limitata di ultima generazione, quelli che girano a 2 km di risoluzione orizzontale, riusciranno a vedere con buona precisione anche molte valli alpine. Il termine “grossolano” sta ad indicare che per il modello la montagna sarà più bassa e più larga. Tanto più la risoluzione orizzontale del grigliato del modello è scarsa, tanto più bassa e larga diverrà la montagna.
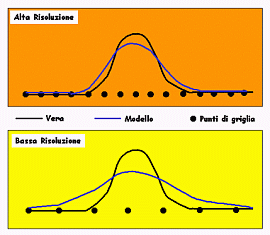
Un esempio pratico è mostrato nella figura allegata all’articolo, in sole due dimensioni per comodità.
Il modello parte da un database digitale di orografia ad alta risoluzione (se ne trovano in rete a circa 1km di risoluzione) sull’area di interesse (l’orografia vera è la linea nera in figura), e deve interpolare questi valori reali sul suo grigliato (i punti neri in figura). Poiché il grigliato del modello non coincide con quello su cui è definita l’orografia, si procede a fare un’interpolazione: preso un punto del modello, si determina la quota nel modello come media delle quote dei punti nel database che stanno vicini. Questo inevitabilmente porta ad un’approssimazione che è ben evidente in figura. Se la griglia del modello ha maglie fitte, l’errore che si compie sarà inferiore, poiché solo pochi punti entreranno nella media che determina l’orografia del modello. Inoltre, per ragioni di rumore nel calcolo numerico, nei modelli si procede anche ad uno ‘smoothing’, cioè ad un ulteriore smussamento di eventuali variazioni troppo brusche della montagna.
Quindi, se consideriamo un modello globale, con punti di griglia distanti 50-100 km, non ci dobbiamo stupire se ci sono errori, a volte grossolani, nel descrivere fenomeni a piccola scala legati alle montagne. Inoltre succede spesso che città che si trovano in prossimità delle montagne, vengano viste dal modello a quote ben diverse dal reale. Città come Torino, Verona, Trento per citarne alcune, ma anche Milano, possono trovarsi a quote ben superiori al vero, proprio perché il modello tende ad allargare la montagna. Quindi c’è da stare sempre molto attenti se si vanno a vedere i valori di campi meteorologici vicino al suolo (temperatura a 2m o vento in superficie) corrispondenti a queste città, derivanti da interpolazione di modelli.