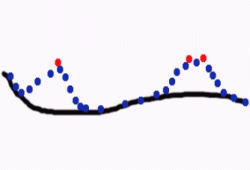
L’algoritmo più semplice per trattare le osservazioni è la Cressman Analysis. Si parte da un valore di background (un tempo la climatologia, ora un first guess del modello) che viene portato progressivamente verso il valore osservato, laddove sia presente la misura. Nella figura allegata all’articolo, la linea nera rappresenta il background e i pallini rossi le osservazioni. La Cressman Analysis produce la linea a pallini blu, che coincide con il background lontano dalle osservazioni, e si rilassa verso i dati dove sono presenti. Quindi in questo esempio, l’unione del first guess del modello e delle osservazioni, genera l’analisi che è la curva a pallini blu.
Chiaramente il metodo è estremamente approssimativo poiché manca il controllo di qualità dei dati, non è chiaro come avviene il rilassamento, non sono garantite relazioni di equilibrio tra le variabili e soprattutto non vengono presi in considerazione i pesi degli errori dei dati e del modello. Però è molto semplice ed intuitivo ed in questo caso a 2 dimensioni è molto didattico.
Passando a metodi recenti e ancora utilizzati, l’Optimal Interpolation rappresenta già una possibilità valida per l’assimilazione. Per capirla faccio un esempio semplicissimo.
Suppongo di avere due misure di temperatura T1 e T2, ognuna con il suo errore e1 ed e2 (per essere precisi e1 ed e2 sarebbero le varianze). L’analisi, ovvero la migliore stima della realtà sarà data da una combinazione delle due temperature:
T=a1T1+a2T2
dove a1 e a2 sono coefficienti che dipendono dall’errore associato a T1 e T2:
a1 = pow2(e2) / (pow2(e1) + pow2(e2))
a2 = pow2(e1) / (pow2(e1) + pow2(e2))
Quindi se la misura T1 ha un grosso errore (pow2(e1) grande), il peso a2 sarà grande e quindi nel determinare T avrà maggiore importanza la misura T2. In pratica il contributo maggiore viene dato dalla componente più precisa, come è logico che sia.
Questo è il concetto. Ora basta pensare che T1 sia il first guess del modello, mentre T2 la misura ed il gioco è fatto. Nella realtà si lavora in 3 dimensioni con matrici molto grosse.
Data la sua relativa semplicità di applicazione, senza richiedere esose capacità computazionali, l’Optimal Interpolation viene utilizzata anche in centri piccoli, e per l’assimilazione in modelli ad area limitata. Infatti questi modelli vengono inizializzati da modelli globali le cui analisi possono essere talvolta carenti nel descrivere particolari a scala fine (mesoscala) data la scarsa risoluzione spaziale del grigliato. Questi dettagli possono essere importanti per i LAM che invece lavorano a risoluzioni più alte. Così, assimilando osservazioni a risoluzione migliore nei LAM si possono recuperare importanti dettagli per migliorane la previsione successiva.
Si arriva così ai metodi più recenti ed avanzati di cui vorrei illustrare solo alcune fondamentali proprietà, senza entrare nei complicatissimi dettagli matematici.
Questi metodi sono metodi 4D, ovvero oltre che nello spazio, lavorano anche nel tempo. Sono metodi di assimilazione dinamica, che sfruttano le proprietà dinamiche del sistema, ovvero ne identificano le instabilità intrinseche che crescono nel tempo più rapidamente. Ciò permette di ottenere un’analisi che non solo è precisa in termini di dettagli dello stato attuale dell’atmosfera, ma che, soprattutto, contiene derivate temporali il più accurate possibili. Quindi nell’analisi è in un qualche modo contenuta la migliore evoluzione possibile del sistema.
Riassumendo quindi, per ottenere l’analisi, ovvero la migliore rappresentazione possibile dello stato dell’atmosfera, i metodi di assimilazione dati uniscono 2 pezzi di informazione. Il primo pezzo deriva dalle osservazioni ed è un campo discontinuo e lacunoso. Il secondo pezzo è ottenuto con una previsione a breve termine del modello, detta first guess, ed è un campo continuo, fisicamente coerente, che permette di utilizzare al meglio le osservazioni e di propagarne l’informazione.
Nel prossimo articolo tratterò della previsione probabilistica ottenuta con la tecnica ensemble:
https://www.meteogiornale.it/news/read.php?id=10145
Legenda
pow2 = potenza al quadrato